Mesh Analysis
Mesh is a loop that doesn’t consists of any other loop inside it. Mesh analysis technique, uses mesh currents as variables , instead of currents in the elements to analyse the circuit. Therefore, this method absolutely reduces the number of equations to be solved . Mesh analysis applies the Kirchhoff’s Voltage Law (KVL) to determine the unknown currents in a given circuit. Mesh analysis is also called as mesh-current method or loop analysis. After finding the mesh currents using KVL, voltages anywhere in a given circuit can be determined by using Ohms law. Back to top
Steps to Analyse the mesh analysis technique
- Check whether there is a possibility to transform all current sources in the given circuit to voltage sources.
- Assign the current directions to each mesh in a given circuit and follow the same direction for each mesh.
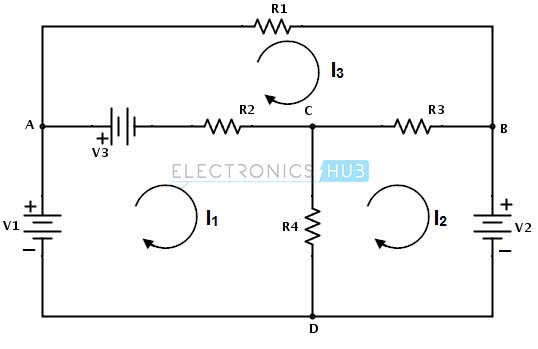
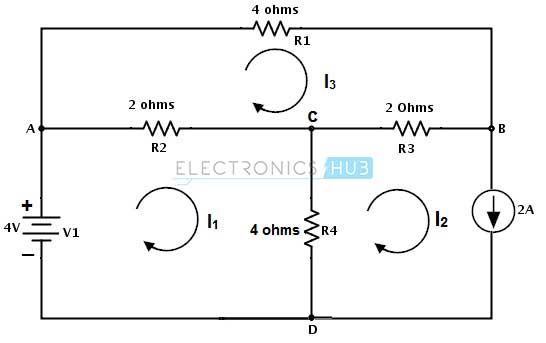
- Apply KVL to each mesh and simplify the KVL equations. 4) Solve the simultaneous equations of various meshes to get the mesh currents and these equations are exactly equal to the number of meshes present in the network. Consider the below DC circuit to apply the mesh current analysis, such that currents in different meshes can be found. In the below figure there are three meshes present as ACDA, CBDC and ABCA but the path ABDA is not a mesh. As a first step, the current through each mesh is assigned with the same direction as shown in figure.
Secondly, for each mesh we have to apply KVL. By applying KVL around the first loop or mesh we get V1 − V3 − R2 ( I1 − I 3 ) − R4 ( I1 − I 2 ) = 0 V1 − V3 = I1 ( R2 + R4 ) − I2R4 − I3R2 ………………(1) Similarly , by applying KVL around second mesh we get, −V2 − R3 ( I 2 − I 3 ) − R4 ( I 2 − I1 ) = 0 − V2 = − I1R4 + I 2 ( R3 + R4 ) − I 3 R3 ………………………(2) And by applying KVL around third mesh or loop we get, V3 − R1I 3 − R3( I 3 − I 2 ) − R2( I 3 − I1 ) = 0 V3 = − I1R2 − I2R3 + I3(R1 + R2 + R3) ………………………(3) Therefore, by solving the above three equations we can obtain the mesh currents for each mesh in the given circuit. Back to top
Example problems on mesh analysis:
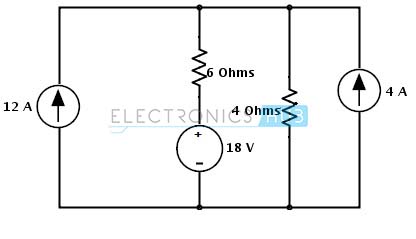
Example 1: Consider the below example in which we find the voltage across the 12A current source using mesh analysis. In the given circuit all the sources are current sources.
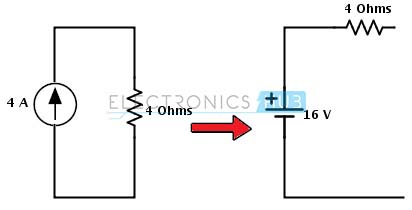
Step 1: In the circuit there is a possibility to change the current source to a voltage source on right hand side source with parallel resistance. The current source is converted into a voltage source by placing the same value of resistor in series with a voltage source and the voltage in that source is determined as Vs = Is Rs = 4× 4 = 16 Volts
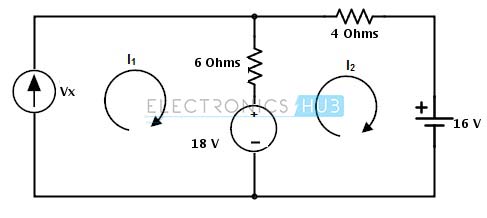
Step 2: Assign the branch currents as I1 and I2 to the respective branches or loops and represent the direction of currents as shown below.
Step 3: Apply the KVL to each mesh in the given circuit Mesh -1: Vx − 6 × (I1 − I 2) − 18 = 0 Substituting I1 = 12 A Vx + 6I2 = 90…………………… (1) Mesh – 2: 18 − 6 × ( I 2 − I1 ) − 4 × I 2 − 16 = 0 2 – 10 × I2 + 6(12) = 0 I2 = 74/ 10 = 7.4 Amps Substituting in equation 1 we get Vx = 90 – 44.4 = 45.6 Volts Example 2: Consider the below circuit where we determine the voltage across the current source and a branch current Iac. Assign the directions as shown below and note that current is assigned opposite to the source current in second loop. By applying KVL to the first mesh we get V1 − R2 ( I1 − I 3 ) − R4 ( I1 − I 2 ) = 0
4 – 2 I1 − 2I3 − 4I1 − 4I2 = 0 -6I1 − 2I3 = 4 ……………(1) By applying KVL to the second mesh we get −Vc − R4( I 2 − I1 ) − R3 ( I 2 − I 3 ) = 0 – Vc = 4I2 − 4I1 + 2I2 − 2I3 = 0 – Vc = – 4I1 + 6I2 – 2I3 But I2 = -2 A, then – Vc = – 4I1 – 12 – 2 I3 ………………….(2) By applying KVL to the third mesh we get − R1 I 3 − R3 ( I 3 − I 2 ) − R2 ( I 3 − I1 ) = 0 −4 I3 − 2I3 + 2I2 − 2I3 + 2I1 = 0 − 8I3 − 4 + 2I1 = 0 (by substituting I2 = -2 A) 2I1 − 8I3 = 4 …………………(3) By solving 1 and 3 equations we get I3 = -0.615 and I1 = 4.46 Therefore, the voltage Vc = 4 (4.46) + 12 + 2(-0.615) Vc = 28.61 V And the branch current Iac = I1- I3 Iac = 5.075 amps Likewise we can find every branch current using the mesh analysis. Back to top
Super Mesh Analysis
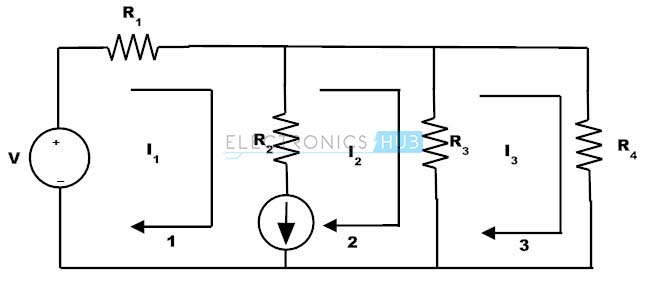
As we seen in the example 2, it contains current source in one of its branches. And before the application of the mesh analysis to that circuit, we assumed the unknown voltage across the current source and then mesh analysis is applied. This is a quite difficult approach and this can be overcome by applying supermesh technique. A super mesh is formed when two adjacent meshes share a common current source and none of these (adjacent) meshes contains a current source in the outer loop. Consider the below circuit in which super mesh is formed by the loop around the current source.
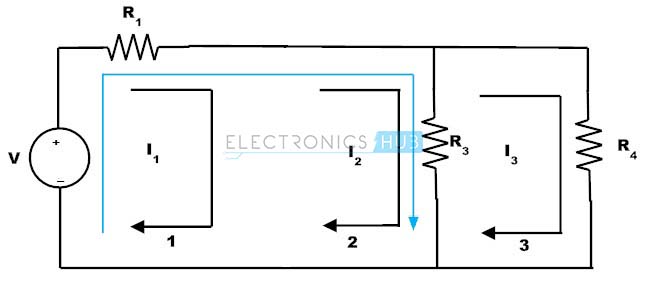
The current source is common to the meshes 1 and 2 and hence it must be analysed independently. To achieve this, assume the branch that contains current source is open circuited and create a new mesh called super mesh.
Writing KVL to the super mesh we get V = I1R1 + (I2 – I3) R3 = I1R1 + I2R3 – I3R3 Applying KVL to the Mesh 3 we get (I3 – I2) R3 + I3R4 = 0 And the difference between the two mesh currents gives the current from the current source. Here the current source direction is in the loop current direction I1. Hence I1 is more than I2, then I = I1 – I2 Thus, by using these three mesh equations we can easily find the three unknown currents in the network. Back to top
Example on supermesh analysis
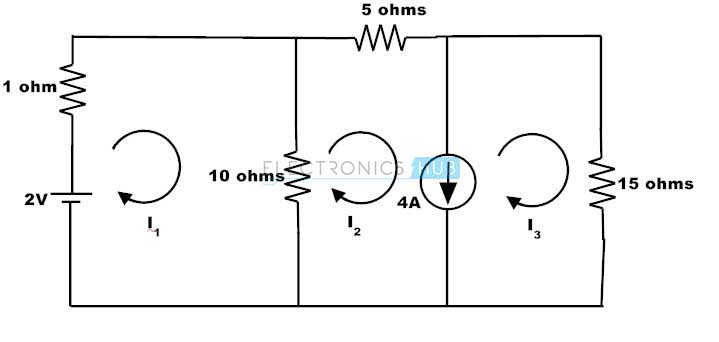
Consider the below example in which we have to find the current through the 10 ohms resistor.
By applying the KVL to the mesh 1 we get 1I1 + 10 (I1 – I2) = 2 11I1 – 10 I2 = 2 …………………………. (1) The meshes 2 and 3 consist of 4A current source and hence form a super mesh. The current from 4A current source is in the direction of I3 and thus the super mesh current is given as I = I3 – I2 I3 – I2 = 4…………………………. (2) By applying KVL to the outer loop of the super mesh we get, – 10 (I2 – I1) – 5I2 – 15I3 = 0 10I1 – 15I2 – 15I3 = 0…………………….. (3) By solving 1, 2 and 3 equations, we get I1 = –2.35 A I2 = –2.78 A I3 = 1.22 A Hence the current through the 10 ohms resistor is I1 – I2 = –2.35 + 2.78 A = 0.43 A Back to top Comment * Name * Email * Website
Δ





![]()